1. 论文信息

论文标题：《Shape-Adaptive Selection and Measurement for Oriented Object Detection》

论文发表：AAAI 2022
论文链接：https://ojs.aaai.org/index.php/AAAI/article/view/19975
论文代码：https://github.com/houliping/SASM

@inproceedings{hou2022shape,
  title={Shape-adaptive selection and measurement for oriented object detection},
  author={Hou, Liping and Lu, Ke and Xue, Jian and Li, Yuqiu},
  booktitle={Proceedings of the AAAI Conference on Artificial Intelligence},
  volume={36},
  number={1},
  pages={923--932},
  year={2022}
}

Name	Value
标签	#标签分配 #旋转目标检测
数据集	#DOTA #HRSC2016 #UCAS-AOD #ICDAR2015
目的	解决旋转目标检测中样本选择没有考虑目标形状信息、没有区分不同质量正样本的问题
方法	提出shape-adaptive selection以及shape-adaptive measurement

2. 问题背景

作者提到旋转目标检测仍然面临挑战，其中最主要的挑战来自目标的形状（如长宽比）。在通用目标检测任务中，样本选择（sample selection，也叫标签分配，label assignment）对于性能提升具有重要作用。然而现有的样本选择策略存在以下不足：

忽视了目标的形状信息
没有对选择的正样本的做潜在的区分
大多数方法只能用于anchor-free或者anchor-based，不能同时适用

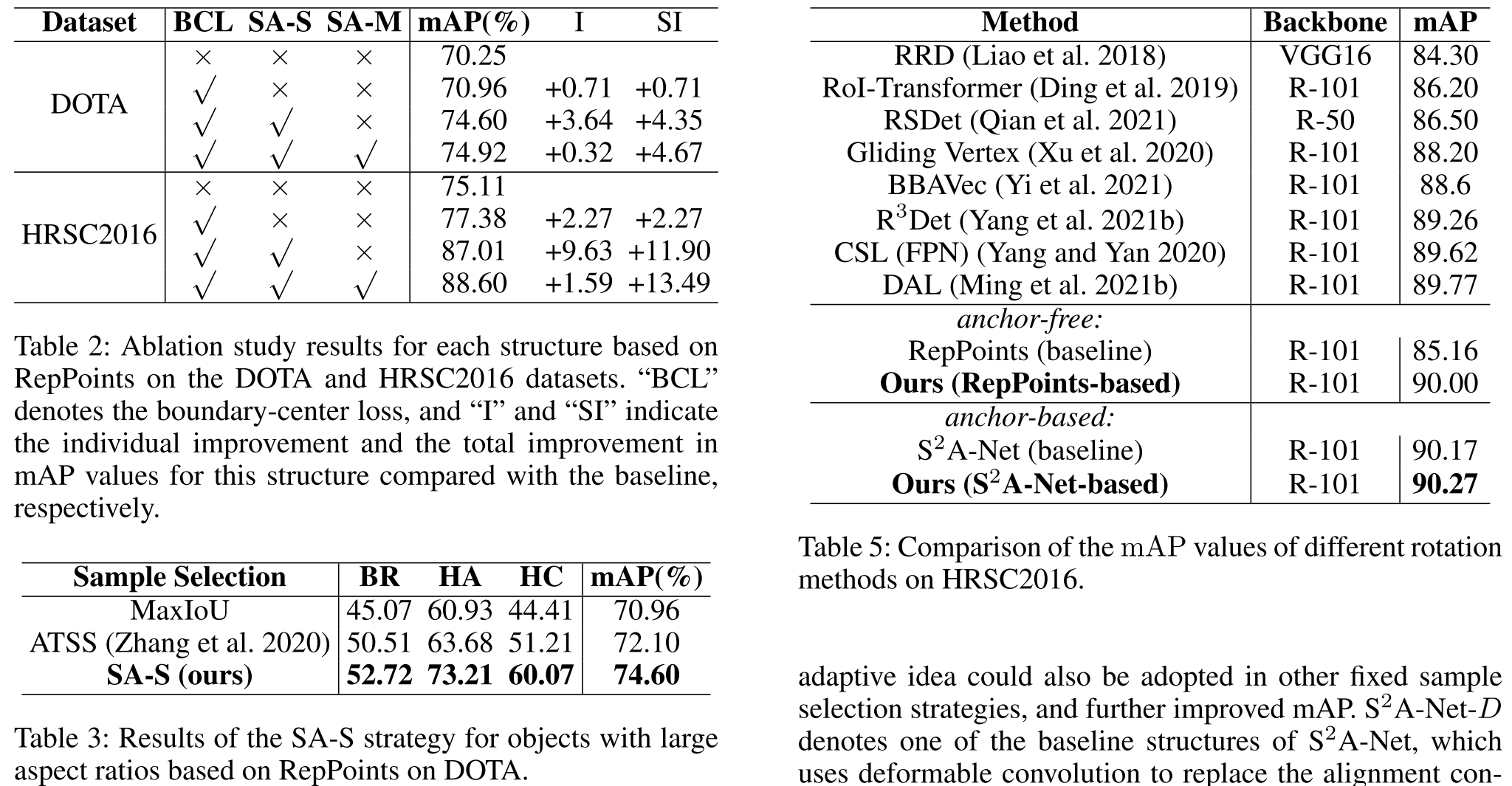
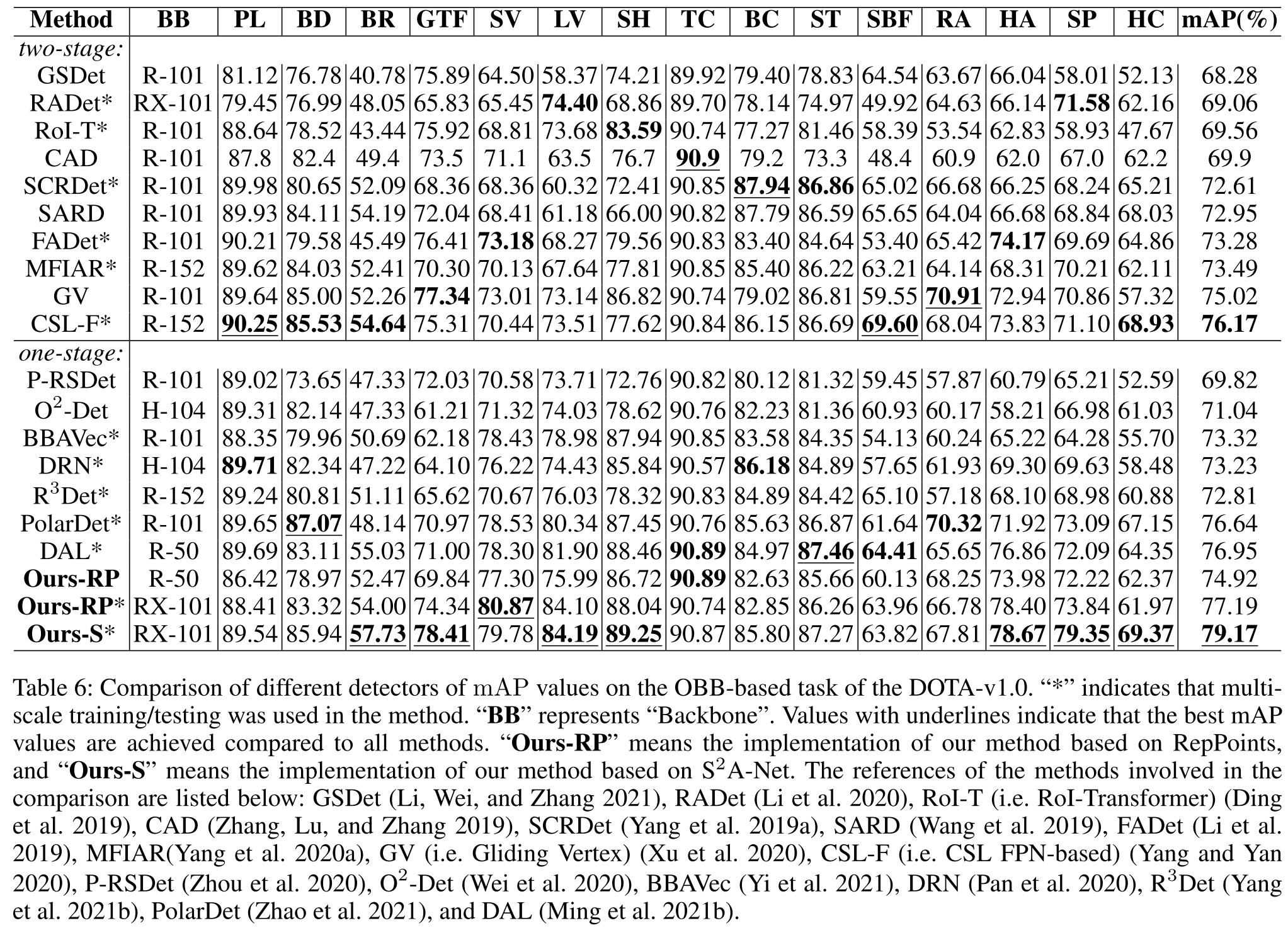
3. 主要工作

针对上述问题，作者提出了shape-adaptive selection（SA-S）和shape-adaptive measurement（SA-M）策略。

SA-S：根据目标形状信息和特征分布动态地选择样本
SA-M：度量定位能力，针对所选正样本增加质量信息

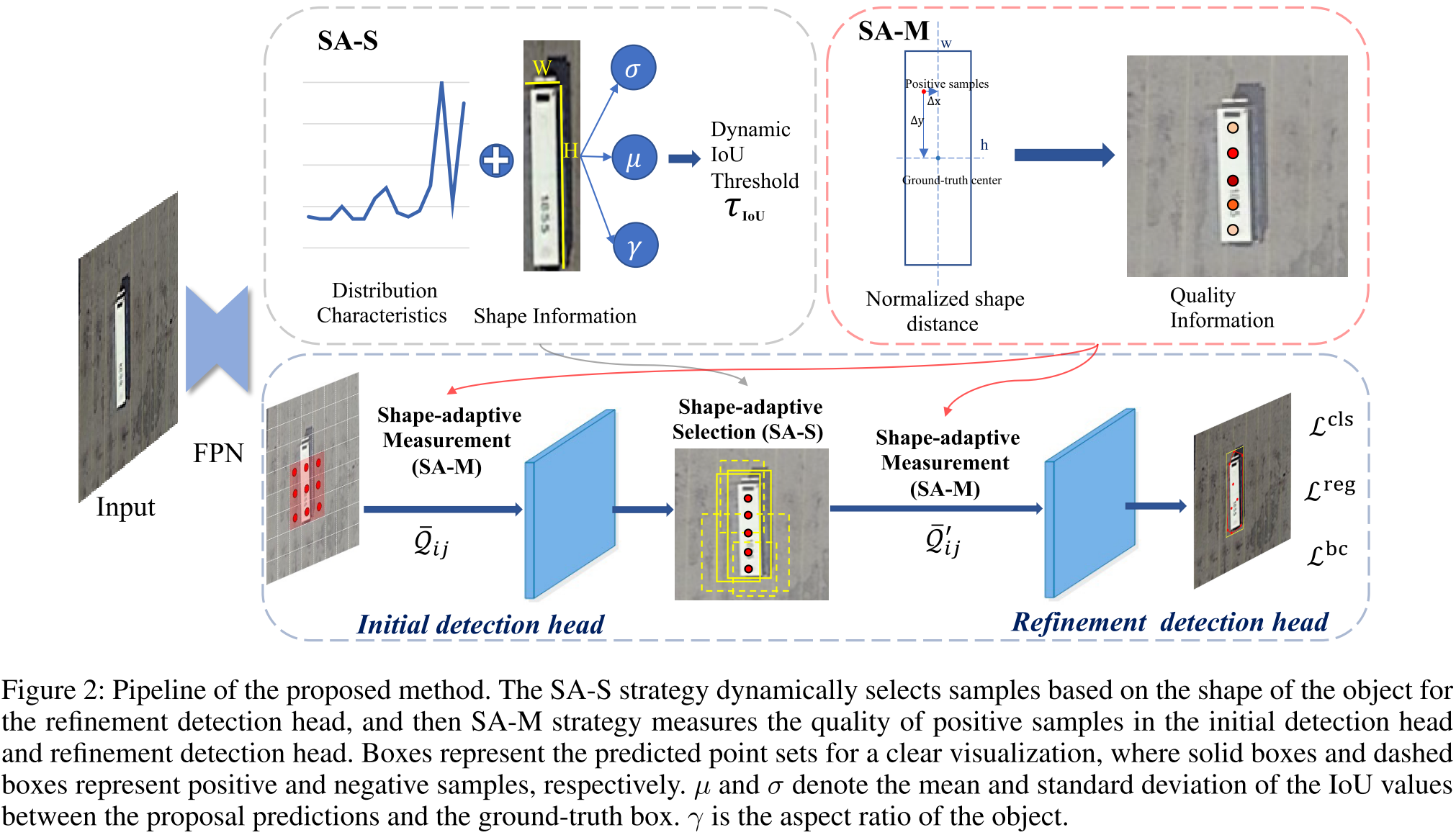
3.1 模型结构

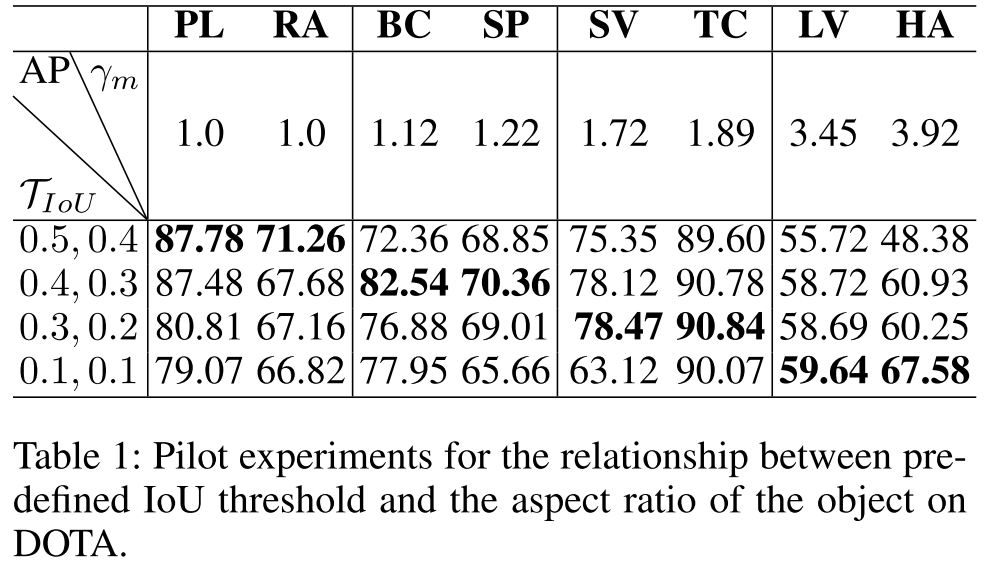
3.2 Motivation

作者做了一个实验，分析不同正负样本IoU划分阈值对不同长宽比类别性能的影响，可以发现当长宽比变大时，IoU阈值越小越好，这可以说明传统的固定IoU阈值的划分方式并不是最优的。

3.3 Shape-Adaptive Selection

根据ATSS，目标真值和预测值的IoU均值和方法可以用于计算动态的IoU阈值，因此对于第i个真值框，IoU阈值可以计算为:
$$\tau_i^{IoU}=f(y_i)\times(\mu+\sigma)$$

其中:
$$\mu = \frac{1}{J}\sum\limits^{J} _ {j=1} I _ {i,j}$$

而
$$\sigma=\sqrt{\frac{1}{J}\sum _ {j=1}^J(I _ {i,j}-\mu)^2}$$

其中J是候选样本的数量，$I_{i,j}$是第i个真值框和第j个预测框之间的IoU值，$y_{i}$代表真值框的长宽比。根据上面的分析，权重应该随着纵横比的增加而减小，因此长宽比较大的目标被分配一个较低的IoU阈值，故而:
$$f(y_i)=e^{-\frac{y_i}{\omega}}$$

其中ω是一个权重参数，默认为4。当数据集包含大量大长宽比目标时，较大的ω通常可以获得更好的性能。这样，当IoU大于等于$\tau_i^{IoU}$时，认为其是正样本。

3.4 Shape-Adaptive Measurement

作者认为与位于物体内部的点相比，位于物体边界附近的点包含更多关于杂波背景，甚至附近物体的信息。因此，位于物体内部的点，特别是位于物体中心周围的点，比位于物体边界附近的点更能代表物体的特征。因此如果用所有正样本都有同样的权重会导致一些高质量正样本被远离物体中心的低质量样本点抑制，且每个样本点的质量与物体的形状密切相关，而不仅仅与每个点到物体中心的距离有关。

因此作者提出了一种基于归一化形状距离的Shape-Adaptive Measurement策略。其具体做法如下：
针对每一个真值框$(x,y,w,h,\theta)$，其分别代表中心点坐标，宽度，高度和角度。归一化形状距离计算如下：
$$
\Delta d _ {ij}=
\begin{equation}
\begin{array}{lr}
\sqrt{\frac{(x _ i-x _ j)^2}{w _ i}+\frac{(y _ i-y _ j)^2}{h _ i}}, & 0\leqslant\theta _ i\leqslant\frac{\pi}{2} \\
\sqrt{\frac{(x _ i-x _ j)^2}{h _ i}+\frac{(y _ i-y _ j)^2}{w _ i}}, & otherwise
\end{array}
\end{equation}
$$
正样本的质量计算为$\bar{Q} _ {ij}=e^{-\Delta{d _ {ij}}}$.

3.5 损失函数

作者认为较大偏差的孤立点会极大地影响凸包(convex hull，其由预测点集计算得到)的质量，并对精确定位产生不利影响，因此提出了边界中心损失（Boundary-Center Loss），其从点集中选取最左点、最右点、最上点和最下点，用点集中所有点的x坐标和y坐标的平均值来计算平均中心点：
$$L^{bc}=\sum\limits _ {i=1}^{5}L _ {smooth}(p _ i,g _ i)$$

因此总损失为：
$$L=\lambda _ 1L^c+\lambda _ 2L^1+\lambda _ 3L^2$$

其中$L^c,L^1,L^2$分别代表分类损失，初始检测损失，精炼检测损失。$\lambda_1,\lambda_2,\lambda_3$是权重系数，根据经验设为1.0，0.375和1.0. 其中分类损失计算为：
$$L _ i^c=\frac{1}{N^+}\frac{1}{\sum _ {p _ j\in{P^+}}\bar{Q} _ {ij}}\sum\limits _ {ij}\bar{Q} _ {ij}$$

其中$j,N^+,P^+$分别代表序号，总数和预测值。$L^{cls}$代表focal loss。
初始检测损失为：
$$L^1 _ i=\frac{1}{N^+}\frac{1}{\sum _ {p _ j\in{P^+}}\bar{Q} _ {ij}}\sum\limits _ {ij}\bar{Q} _ {ij}L _ {ij}^{reg}+L^{bc} _ {ij}$$

其中$L^{reg}=1-GIoU$代表GIoU Loss。
精炼阶段检测损失为：
$$L^2 _ i=\frac{1}{N^+}\frac{1}{\sum _ {p _ j\in{P^+}}\bar{Q} _ {ij}}\sum\limits _ {ij}\bar{Q} _ {ij}L _ {ij}^{reg}$$