深度学习

第一章前言

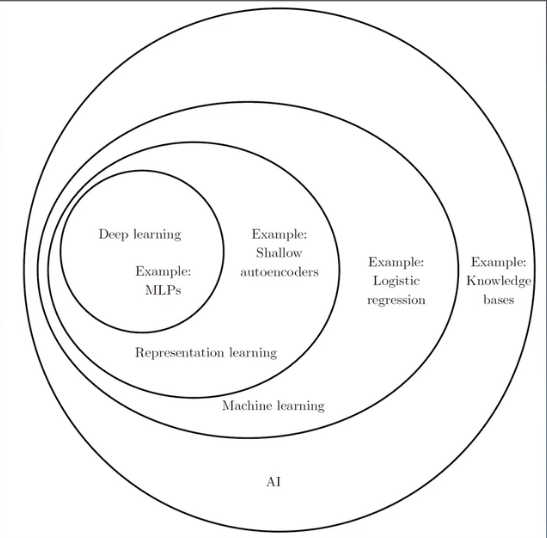
深度学习(Deep Learning) ∈ 表示学习(Representation Learning) ∈ 机器学习(Machine Learning) ∈ 人工智能(AI)

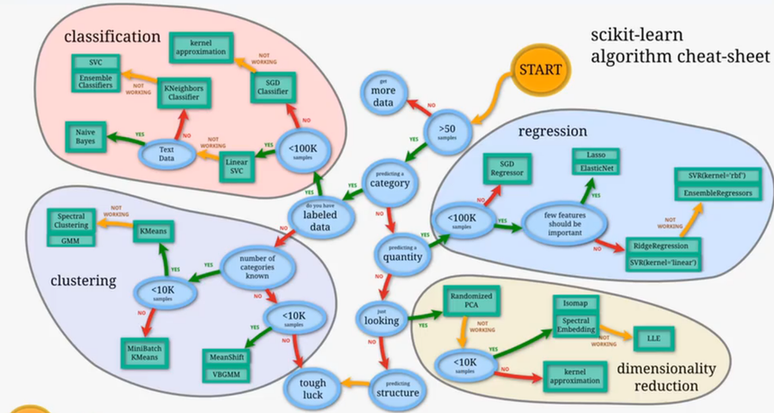
分类，回归，聚类，降维

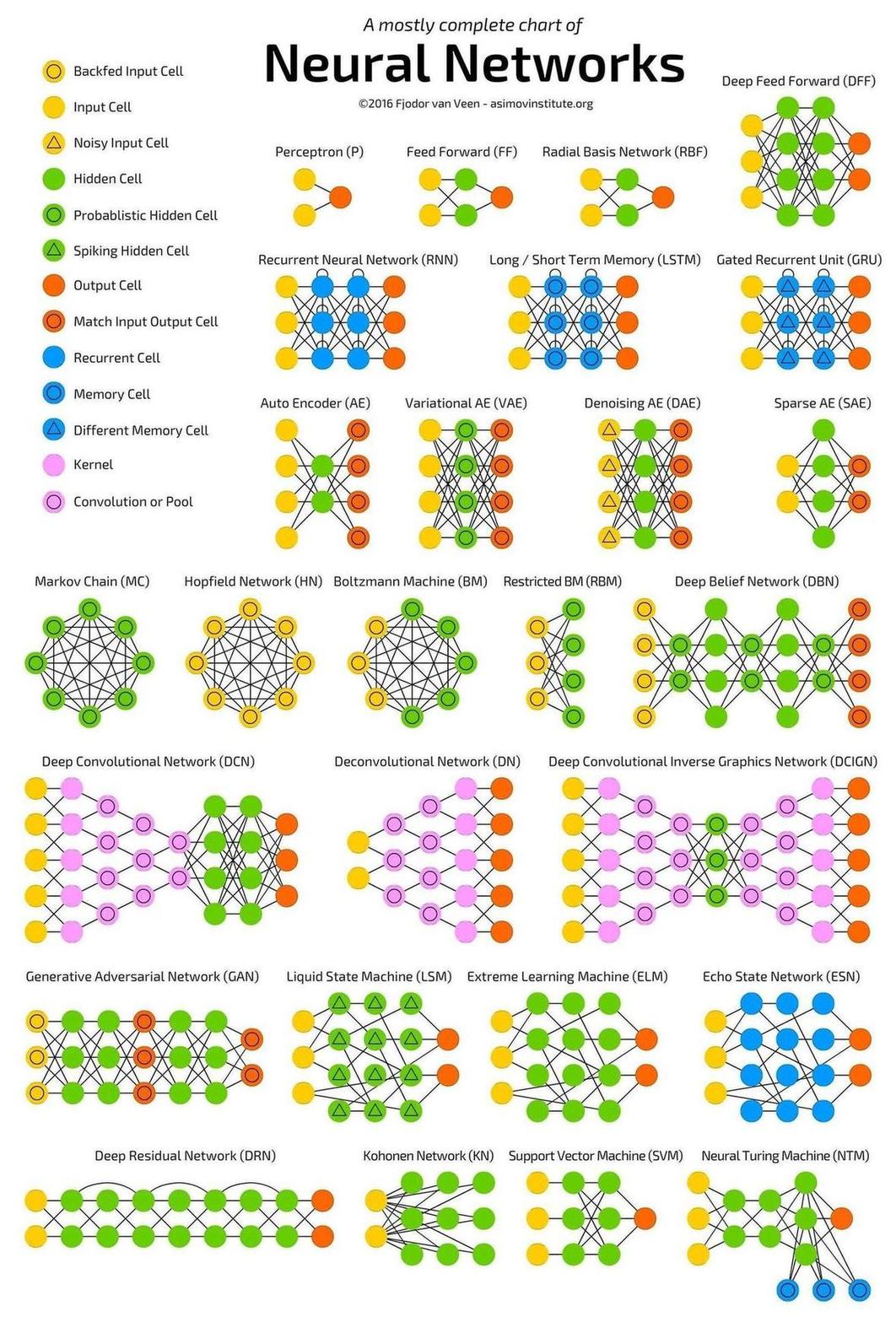
神经网络

第一部分应用数学与机器学习基础

第二章线性代数

2.1 标量，向量，矩阵和张量

1.标量(scalar)是一个单独的数
2.向量(vector)是一列数，这些数是有序排列的

$$
x = \begin{bmatrix}
x_1\
x_2\
\vdots\
x_n\
\end{bmatrix}
$$

3.矩阵(matrix)是一个二维数组

$$
\begin{bmatrix}
A_{1,1} & A_{1,2}\
B_{2,1} & B_{2,2}\
\end{bmatrix}
$$

4.张量(tensor)：一般将超过二维的数组称为张量

转置：以对角线为轴的镜像

$$
(A^T){i,j}=A{j,i}
$$

广播：将一个向量隐式的复制到每一行生成矩阵（用于运算）的方式

$$C=A+b$$
$$C_{i,j}=A_{i,j}+b$$
$$
\begin{bmatrix}
C_{1,1} & C_{1,2} & C_{1,3}\
C_{2,1} & C_{2,2} & C_{2,3}\
C_{3,1} & C_{3,2} & C_{3,3}\
\end{bmatrix}=
\begin{bmatrix}
A_{1,1} & A_{1,2} & A_{1,3}\
A_{2,1} & A_{2,2} & A_{2,3}\
A_{3,1} & A_{3,2} & A_{3,3}\
\end{bmatrix}+
\begin{bmatrix}
b_{1} & b_{2} & b_{3}\
\end{bmatrix}=
\begin{bmatrix}
A_{1,1} & A_{1,2} & A_{1,3}\
A_{2,1} & A_{2,2} & A_{2,3}\
A_{3,1} & A_{3,2} & A_{3,3}\
\end{bmatrix}+
\begin{bmatrix}
b_{1} & b_{2} & b_{3}\
b_{1} & b_{2} & b_{3}\
b_{1} & b_{2} & b_{3}\
\end{bmatrix}
$$

2.2 矩阵和向量相乘

如果A的形状是m×n，B的形状是n×p，C=AB，那么C的形状是m×p
具体地，该乘法操作定义为：
$$C_{i,j}=\sum_kA_{i,k}B_{k,j}$$

注意区分：存在一种两个矩阵对应元素的乘积，叫Hadamard乘积，记为A⊙B

性质：

分配律
$$A(B+C)=AB+AC$$
结合律
$$A(BC)=(AB)C$$
矩阵乘积不具有交换律，但是两个向量的点积满足交换律
$$x^Ty=y^Tx$$
$$(AB)^T=B^TA^T$$

对于AX=b，可表示
$$A_{1,1}x_1+A_{1,2}x_2+\cdots+A_{1,n}x_n=b_1$$
$$A_{2,1}x_1+A_{2,2}x_2+\cdots+A_{2,n}x_n=b_2$$
$$\vdots$$
$$A_{m,1}x_1+A_{m,2}x_2+\cdots+A_{m,n}x_n=b_m$$
即
$$
\begin{bmatrix}
A_{1,1} & A_{1,2} & \cdots & A_{1,n}\
A_{2,1} & A_{2,2} & \cdots & A_{2,n}\
\vdots\
A_{m,1} & A_{m,2} & \cdots & A_{m,n}\
\end{bmatrix}
\begin{bmatrix}
x_{1}\
x_{2}\
\vdots\
x_{n}\
\end{bmatrix}=
\begin{bmatrix}
b_{1}\
b_{2}\
\vdots\
b_{m}\
\end{bmatrix}
$$

2.3 单位矩阵和逆矩阵

单位矩阵：任何向量和单位矩阵相乘，都不会改变
$${\forall}x{\in}R^n,I_nx=x$$

$$I_3=
\begin{bmatrix}
1 & 0 & 0\
0 & 1 & 0\
0 & 0 & 1\
\end{bmatrix}
$$
矩阵逆，记作$$A^{-1}$$，定义
$$A^{-1}A=I_n$$

2.4 线性相关和生成子空间

对于矩阵逆的定义：
$$A^{-1}A=I_n$$
可以通过以下步骤求解：
$$Ax=b$$
$$A^{-1}Ax=A^{-1}b$$
$$I_nx=A^{-1}b$$
$$x=A^{-1}b$$
如果能找到一个逆矩阵$A^{-1}$，那么若$s=w_1x_1+w_2x_2+{\cdots}+w_kx_k$。s变量是对变量x的加权线性”混合”。因此，将s定义为变量的线性组合。

生成子空间：原始向量的一切线性组合生成的子空间
线性无关：一组向量中的任意一个向量都不能表示成其他向量的线性组合，那么这组向量被称为线性无关

如果数组向量中的某一个或多个向量可以由数组内的其余向量通过加法或数乘表达，则该向量组线性相关，反之则线性无关。

方阵：行列大小相同的矩阵

2.5 范数

为了衡量一个向量的大小，在机器学习中，我们经常使用范数（norm）的函数衡量。形式上，$L^p$范数定义如下：
$$
\left | x \right | _ p=\left ( \sum_i\left | x_i \right |^p\right )^\frac{1}{p}
$$
其中$p \in \mathbb{R},p \geqslant 1$

范数，是将向量映射到非负值的函数。直观上来说，向量x的范数衡量从原点到点x的距离。更严格的说，范数是满足下列性质的任意函数：
$$f\left (x \right )=0\Rightarrow x=0$$
$$
f\left (x + y \right )\leqslant f \left ( x \right ) + f\left(y \right)
$$

$$
\forall \alpha \in \mathbb{R},f({\alpha}x)=|\alpha|f(x)
$$

当p=2时，$L^2$范数被称为欧几里得范数。平方$L^2$范数，也经常用来衡量向量的大小。
$L^1$范数的定义，$||x|| _ 1 = \sum_i|x_i|$
另一个常在机器学习中出现的范数是$L^∞$范数，也被称为最大范数。这个范数表示向量中具有最大幅值的元素的绝对值：
$$||x|| _ ∞ =\max_i|x_i|$$
Frobenius范数：$$\left |A\right | _ F = \sqrt{\sum _ {i,j}{A^2} _ {i,j}}$$

两个向量的点积，可以用范数来表示：
$$x^Ty=||x|| _ 2 ||y|| _ 2 \cos \theta $$
其中$\theta$，表示x和y之间的夹角

2.6 特殊类型的矩阵和向量

对角矩阵:只在主对角线上含有非零元素，其他位置都是零的矩阵。单位矩阵是对角元素都为1的对角矩阵。

如果用diag(v)表示一个对角元素由向量v中的元素给定的对角方阵,那么$diag(v)x=v\odot x$，并且计算对角方阵的逆矩阵也很高效，如果对角方阵的逆矩阵存在，当且仅当对角元素都是非零值，这种情况下有，$diag(v)^{-1}=diag([\frac{1}{v_1},\cdots,\frac{1}{v_n}]^T)$
不是所有的对角矩阵都是方阵，非方阵的对角矩阵没有逆矩阵

对称矩阵是转置和自己相等的矩阵
$$A=A^T$$

单位向量是具有单位范数的向量
$$||x|| _ 2 = 1$$

正交：如果$x^Ty=0$，那么向量x和向量y互相正交，如果两个向量都有非零范数，那么他们之间的夹角为90度。
标准正交：如果这些向量的不仅互相正交，并且范数都为1，那么我们称他们为标准正交
正交矩阵：指行向量和列向量是分别标准正交的方针
$$A^TA=AA^T=I$$
$$A^{-1}=A^T$$

补充关于点乘和叉乘：
点乘，也叫数量积，结果是一个向量在另一个向量方向上的投影的长度，是一个标量；
$A·B=|A||B|\cos\theta$，点积为0，说明两个向量正交
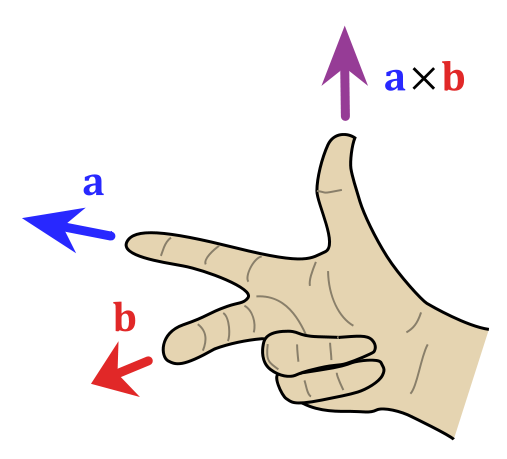
叉乘，也叫向量积，结果是一个和已有两个向量都垂直的向量，向量模长是向量A，B组成平行四边形的面积，即$\left | A×B\right|=\left|A \right|\left|B \right|\sin\theta$；向量方向垂直于向量A,B组成的平面；
$$A×B=\begin{vmatrix}
i & j & k\
a_1 & a_2 & a_3\
b_1 & b_2 & b_3
\end{vmatrix}=
\begin{vmatrix}
a_2 & a_3\
b_2 & b_3
\end{vmatrix}i-
\begin{vmatrix}
a_1 & a_3\
b_1 & b_3
\end{vmatrix}j+
\begin{vmatrix}
a_1 & a_2\
b_1 & b_2
\end{vmatrix}k$$

2.7 特征分解

特征分解是使用最广的矩阵分解之一，即我们将矩阵分解成一组特征向量和特征值

方阵A的特征向量是指与A相乘后相当于对该向量进行缩放的非零向量v：$Av=λv$

$({\lambda}E-A)v=0$，求特征值$\lambda$，其中$|{\lambda}E-A|$被称为特征多项式

标量λ被称为这个特征向量对应的特征值。如果v是A的特征向量，那么任何缩放后的向量sv（s∈R，s≠0）也是A的特征向量。此外sv和v有相同的特征值。

假设矩阵A有n个线性无关的特征向量

$$v^{(1)},\cdots,v^{(n)}$$

对应着特征值

$${\lambda} _ 1,\cdots,{\lambda} _ n$$

将特征向量连接成一个矩阵，使得每一列是一个特征向量：

$$V=[v^{(1)},\cdots,v^{(n)}]$$

类似地，将特征值连接成一个向量

$$\lambda =[{\lambda} _ 1,\cdots,{\lambda} _ n]^T$$

因此A的特征分解可以记作：

$$A=Vdiag(\lambda)V^{-1}$$

特征分解唯一当且仅当所有的特征值都是唯一的
矩阵是奇异的当且仅当含有零特征值（奇异：非满秩）
正定（所有特征值为正），半正定（所有特征值非负），负定（所有特征值为负），半负定（所有特征值非正）

对于每个实对称矩阵，都可以分解成实特征向量和实特征值
$$A=QΛQ^T$$
其中Ｑ是Ａ的特征向量组成的正交矩阵，Λ是对角矩阵。特征值$Λ_{i,j}$对应的特征向量是矩阵Q的第i列，记作$Q_{:,j}$

2.8 奇异值分解

奇异值分解视频

奇异值分解：将矩阵分解为奇异向量和奇异值
假设A是一个m×n的矩阵，那么U是一个m×m的矩阵，D是一个m×n的矩阵，V是一个n×n的矩阵，其中U和V是正交矩阵，D是对角矩阵（不一定是方阵）
$$A=UDV^T$$
对角矩阵D对角线上的元素被称为矩阵A的奇异值，矩阵U的列向量被称为左奇异向量(是$AA^T$的特征向量)，矩阵V的列向量被称为右奇异向量（是$A^TA$的特征向量）。A的非零奇异值是$A^TA$特征值的平方根，也是$AA^T$特征值的平方根

正交-对角-正交：旋转-拉伸-旋转

$$A^TA=(VD^TU^T)(UDV^T)=V(D^TD)V^T$$
$$AA^T=(UDV^T)(VD^TU^T)=U(D^TD)U^T$$
$$A=
\begin{bmatrix}
u_1 & u_2
\end{bmatrix}
\begin{bmatrix}
\sigma_1 & \
& \sigma_2
\end{bmatrix}
\begin{bmatrix}
v_1^T\
v_2^T
\end{bmatrix}
$$

例子：

$$A=\begin{bmatrix}
2 & 2\
1 & 1
\end{bmatrix}=
\begin{bmatrix}
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}}\
\frac{-1}{\sqrt{5}} & \frac{2}{\sqrt{5}}
\end{bmatrix}
\begin{bmatrix}
\sqrt{10} & \
& 0
\end{bmatrix}
\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\
\frac{1}{\sqrt{2}} & \frac{-1}{\sqrt{2}}
\end{bmatrix}
$$

2.9 Moore-Penrose伪逆

对于非方阵，将矩阵A 的伪逆定义为：
$$A^+=\lim_{a\rightarrow0}(A^TA+{\alpha}I)^{-1}A^T$$
实际计算公式
$$A^+=VD^+U^T$$
其中，矩阵U，D和V是矩阵A奇异值分解后得到的矩阵，对角矩阵D的伪逆$D^+$是其非零元素取倒数之后再转置得到的

2.10 迹运算

迹运算返回的是矩阵对角元素的和：
$$Tr(A)=\sum_iA_{i,i}$$

迹运算提供了另一种描述矩阵Frobenius范数的方式$$\left|A\right|F=\sqrt{Tr(AA^T)}$$
迹运算在转置条件下是不变的
$$Tr(A)=Tr(A^T)$$
如果多个矩阵相乘交换顺序后仍有定义，那么有
$$Tr(ABC)=Tr(CAB)=Tr(BCA)$$
$$Tr(\prod{i=1}^{n}F^{(i)})=Tr(F^{(n)}\prod_{i=1}^{n-1}F^{(i)})$$
标量的迹运算还是它自己

2.11 行列式

记作det(A),是一个将方阵A映射到实数的函数。行列式等于矩阵特征值的乘积

2.12 实例：主成分分析

主成分分析（PCA,Principle component analysis）是一个简单的机器学习算法，可以通过基础的线性代数知识推导。

假设，在$\mathbb{R}^n$空间中我们有m个点，为了对这些点进行有损压缩，可以采取低维表示（线性降维），对于每个点$x^{(i)}\in \mathbb{R}^n$,会有一个对应的编码向量$c^{(i)}\in \mathbb{R}^l$。如果l比n小，那么便实现了压缩。需要设置一个编码函数，根据输入返回编码$f(x)=c$，也希望设置一个解码函数，给定编码重构输入$x≈g(f(x))$，为了简化解码器，使用矩阵乘法将编码映射回$\mathbb{R}^n$，即g(c)=Dc，其中D∈$\mathbb{R}^{n×l}$是定义解码的矩阵

首先，我们需要明确如何根据每一个输入x得到一个最优编码
$$c ^ $$
一种方法是最小化原始输入向量x和重构向量
$$g(c^)$$
之间的距离,在PCA中，我们使用L2范数：
$$c ^ * =arg\min _ c \left|x-g(c)\right| _ 2$$

arg min f(x) 是指使得函数 f(x) 取得其最小值的所有自变量 x 的集合。

当然也可以用平方L2范数来替代L2范数：
$$c^*=arg\min_c\left|x-g(c)\right|2^2$$
该最小化函数可以简化成：
$$(x-g(c))^T(x-g(c))$$
$$=x^Tx-x^Tg(c)-g(c)^Tx+g(c)^Tg(c)$$
$$=x^Tx-2x^Tg(c)+g(c)^Tg(c)$$
因为第一项$x^Tx$不依赖于c所以我们可以忽略它，得到：
$$c^*=arg\min_c - 2x^Tg(c)+g(c)^Tg(c)$$
代入g(c)的定义：
$$c^*=arg\min_c - 2x^TDc+c^TD^TDc=arg\min_c - 2x^TDc+c^TI_lc=arg\min_c - 2x^TDc+c^Tc$$
$$\nabla_c(-2x^TDc+c^Tc)=0$$
$$-2D^Tx+2c=0$$
$$c=D^Tx$$
于是，最优编码x只需要一个矩阵-向量乘法操作
$$f(x)=D^Tx$$
PCA重构操作
$$r(x)=g(f(x))=DD^Tx$$
接下来需要挑选编码矩阵D，所以我们需要最小化所有维数和所有点上的误差矩阵的Frobenius范数：
$$D^*=arg\min_D\sqrt{\sum{i,j}(x_j^{(i)}-r(x^{(i)})_j)^2}\text{ subject to } D^TD=I_l$$
先考虑l=1的情况，此时D是一个单一向量d
$$d^*=arg\min_d\sum\left|x^{(i)}-dd^Tx^{(i)}\right|_2^2\text{ subject to } \left|d\right|2=1$$
将表示个点的向量堆叠成一个矩阵，记为X∈$\mathbb{R}^{m×n}$，其中$X{i,:}=x^{(i)^T}$
原问题可以重新表示为：
$$d^*=arg\min_d\left|X-Xdd^T\right|_F^2\text{ subject to }d^Td=1$$
暂不考虑约束，可以把Frobenius范数简化成
$$arg\min_d\left|X-Xdd^T\right|_F^2$$
$$=arg\min_dTr((X-Xdd^T)^T(X-Xdd^T))$$
$$=arg\min_d-2Tr(X^TXdd^T)+Tr(X^TXdd^Tdd^T)$$
再考虑约束条件
$$arg\min_d-2Tr(X^TXdd^T)+Tr(X^TXdd^Tdd^T)\text{ subject to } d^td=1$$
$$=arg\max_dTr(d^TX^TXd)\text{ subject to }d^Td=1$$
即，最优的d是X^TX最大特征值对应的特征向量

PCA算法两种实现方法：
（1）基于特征值分解协方差矩阵实现
输入数据集X={x1,x2,x3,…,xn}，需要降到k维。
1）去平均值（去中心化），即每一位特征减去各自的平均值
2）计算协方差矩阵$\frac{1}{n}XX^T$
3）用特征值分解方法求协方差矩阵的特征值和特征向量
4）对特征值从大到小排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P
5）将数据转换到k个特征向量构建的新空间中，即Y=PX
(2) 基于SVD分解（奇异值分解）协方差矩阵实现PCA算法

第三章概率与信息论

概率论是用于表示不确定性申明的数学框架

3.1 为什么要使用概率

几乎所有的活动都需要能够再不确定性存在时进行推理
不确定性的三种来源：被建模系统内在的随机性，不完全观测，不完全建模

3.2 随机变量

随机变量时可以随机地取不同值的变量。

3.3 概率分布

概率分布用来描述随机变量或一簇随机变量在每一个可能取到的状态的可能性大小

3.3.1 离散型变量和概率质量函数

离散型变量的概率分布可以用概率质量函数(PMF，probability mass function)来描述
联合概率分布是多个变量的概率分布
如果用P表示概率质量函数，则满足以下条件

P的定义域必须是随机变量x所有可能状态的集合
$\forall x \in X, 0 \leq P(x) \leq 1$，不可能发生的事件概率为0，并且不存在比这概率更低的状态。类似的，一定发生的事件概率为1，且不存在比这概率更高的事件。
$\sum_i P(x)=1$

3.3.2 连续型变量和概率密度函数

对于连续型随机变量，用概率密度函数（PDF，probability density function），如果用p表示概率密度函数，则满足以下条件

p的定义域必须是x所有可能状态的集合
$\forall x \in X,p(x) \geq 0$.并不要求p(x)≤1
$\int p(x) \text{d}x = 1$

3.4 边缘概率

边缘概率分布，定义在其中一个子集上的概率分布

$\forall x \in X,P(X=x)=\sum_yP(X=x,Y=y)$
$p(x)=\int p(x,y) \text{d}y$

3.5 条件概率

条件概率，在给定其他事件发生时出现的概率，我们将给定X=x，Y=y发生的条件概率记为P(Y=y|X=x)
计算公式如下
$$P(Y=y|X=x)=\frac{P(Y=y,X=x)}{P(X=x)}$$

条件概率只在P(X=x)＞0时有定义

3.6 条件概率的链式法则

任何多维随机变量的联合概率分布，都可以分解成只有一个变量的条件概率相乘的形式
$$P(x^{(1)},\cdots,x^{(n)})=P(x^{(1)})\prod_{i=2}^{n}P(x^{(i)}|x^{(1)},\cdots,x^{(i-1)})$$

例如：
P(a,b,c)=P(a|b,c)P(b,c)
P(b,c)=P(b|c)P(c)
P(a,b,c)=P(a|b,c)P(b|c)P(c)

3.7 独立性和条件独立性

相互独立：两个随机变量x，y的概率分布可以表示为两个因子的乘积形式，并且一个因子只包含x，另一个只包含y，那么这两个随机变量是相互独立的
$$\forall x \in X,y\in Y,p(X=x,Y=y)=p(X=x)p(Y=y)$$

条件独立：如果关于x和y的条件概率分布对于z的每一个值都可以写成乘积的形式，那么这两个随机变量x和y在给定随机变量z时是条件独立的

$$\forall x \in X,y\in Y,z\in Z,p(X=x,Y=y|Z=z)=p(X=x|Z=z)p(Y=y|Z=z)$$

3.8 期望，方差，协方差

（1）期望(expected value)
函数f(x)关于某分布P(x)的期望或者期望值是指，当x由P产生，f作用到x时，f(x)的平均值

离散型随机变量的期望
$$\mathbb{E} _ {x\sim P}[f(x)]=\sum_x P(x)f(x)$$
连续型随机变量的期望
$$\mathbb{E} _ {x\sim P}[f(x)]=\int p(x)f(x)\text{d}x$$

期望是线性的，假设α和β不依赖于x
$$\mathbb{E}_ x[\alpha f(x)+ \beta g(x) ]=\alpha \mathbb{E}_ x[f(x)] +\beta \mathbb{E}_ x[g(x)]$$

（2）方差(variance)
$$Var(f(x))=\mathbb{E}[(f(x)-\mathbb{E}[f(x)])^2]$$

方差的平方根被称为标准差

（3）协方差
$$Cov(f(x),g(y))=\mathbb{E}[(f(x)-\mathbb{E}[f(x)])(g(y)-\mathbb{E}[g(y)])]$$

两个随机变量独立→协方差为0→没有线性关系
但是协方差为0，两个变量不一定独立

协方差矩阵：
$$Cov(x)_ {i,j}=Cov(x_i,x_j)$$
协方差矩阵的对角元是方差：
$$Cov(x_i,x_i)=Var(x_i)$$

3.9 常用概率分布

3.9.1 Bernoulli分布（伯努利分布）

单个二值随机变量的分布，又名两点分布，0-1分布

对于单次随机试验，对于一个随机变量X而言：
$$P(X=1)=p$$
$$P(X=0)=1-p$$
$$P(X=x)=p^x(1-p)^{1-x}$$
$$E(X)=p$$
$$Var(X)=p(1-p)$$
进行一次伯努利试验，成功(X=1)概率为p(0≤p≤1)，失败(X=0)概率为1-p，则称随机变量X服从伯努利分布。伯努利分布是离散型概率分布，其概率质量函数为：

$$f(x)=p^x(1-p)^{1-x}=\left{\begin{matrix}
p \text{ ,if x=1}\
1-p \text{ ,if x=0}\
0 \text{ ,otherwise}
\end{matrix}\right.$$

3.9.2 Multinoulli分布

Multinoulli分布，或称范畴分布，是指在具有k个不同状态的单个离散型随机变量上的分布，其中k是一个有限值

Multinoulli分布是多项式分布（Multinomial distribution）的一个特例。多项式分布是${0,…,n}^k$中的向量的分布，用于表示当对Multinoulli分布采样n次时k个类中的每一个被访问的次数。即n=1的多项式分布是Multinoulli分布。

Multinoulli分布由向量$p∈[0,1]^{k−1}$参数化，其中每一个分量$ p_i $表示第 i 个状态的概率。最后的第k个状态的概率可以通过$1−1^Tp$给出。注意我们必须限制$1^⊤p≤1$。Multinoulli分布经常用来表示对象分类的分布，所以我们很少假设状态 1 具有数值 1 之类的。因此，我们通常不需要去计算 Multinoulli 分布的随机变量的期望和方差。

Bernoulli 分布和 Multinoulli 分布足够用来描述在它们领域内的任意分布。它们能够描述这些分布，不是因为它们特别强大，而是因为它们的领域很简单。它们可以对那些能够将所有的状态进行枚举的离散型随机变量进行建模。当处理的是连续型随机变量时，会有不可数无限多的状态，所以任何通过少量参数描述的概率分布都必须在分布上加以严格的限制。

3.9.3 高斯分布

高斯分布，也叫正态分布

$$N(x;\mu ,\sigma^2 )=\sqrt{\frac{1}{2\pi \sigma^2}}exp(-\frac{1}{2\sigma^2}(x-\mu)^2)$$
$$N(x;\mu ,\sigma^2 )=\sqrt{\frac{1}{2\pi \sigma^2}}e^{(-\frac{1}{2\sigma^2}(x-\mu)^2)}$$

正态分布的概率密度函数的图象的中心峰的x坐标由μ给出，峰的宽度受σ控制
标准正态分布：μ=0，σ=1

$$\mathbb{E}(x)=\mu$$
$$Var(x)=\sigma^2$$

令β为方差的倒数，来控制分布的精度
$$N(x;\mu ,\beta^{-1} )=\sqrt{\frac{\beta}{2\pi}}e^{(-\frac{1}{2}\beta(x-\mu)^2)}$$

正态分布可以推广到$\mathbb{R}^n$空间，这种情况下被称为多维正态分布
$$N(x;\mu ,\sum )=\sqrt{\frac{1}{(2\pi)^ndet(\sum)}}e^{(-\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu))}$$

参数μ仍然表示分布的均值，只不过现在是向量值。参数∑给出了分布的协方差矩阵，但并不是一个很高效的参数化分布的方式，因为要对∑求逆，因此可以使用一个精度矩阵β替换
$$N(x;\mu ,\beta^{-1} )=\sqrt{\frac{det(\beta)}{(2\pi)^n}}e^{(-\frac{1}{2}(x-\mu)^T\beta(x-\mu))}$$

3.9.4 指数分布和Laplace分布

指数分布，可以用来表示事件的时间间隔的概率，可以由泊松分布推导出来

其概率密度函数
$$f(x)=\left{\begin{matrix}
\lambda e^{-\lambda x} , x >0 \
0 , otherwise
\end{matrix}\right.$$
分布函数
$$F(x)=\left{\begin{matrix}
1-\lambda e^{-\lambda x} , x \geqslant 0 \
0 , x＜0
\end{matrix}\right.（\lambda>0）$$

Laplace分布，允许我们在任意一点μ处设置概率质量的峰值
$$Laplace(x;\mu , \gamma ) = \frac{1}{2\gamma}exp(-\frac{|x-\mu|}{\gamma})$$

3.9.5 Dirac分布和经验分布

概率密度函数
$$p(x)=\delta(x-\mu)$$

Dirac分布经常作为经验分布的组成部分出现

3.9.6 分布的混合

潜变量：不能直接观测到的随机变量

高斯混合模型，概率密度的万能近似器

先验概率：在观测到x之前计算的
后验概率：在观测到x之后计算的

3.10 常用函数的有用性质

logistic sigmoid函数,在变量取绝对值很大的正值或负值时出现饱和现象

$$\sigma(x)=\frac{1}{1+e^{-x}}$$

softplus函数,范围（0,∞）

$$\zeta (x)=log(1+e^x)$$

ReLU函数，人工神经网络常用的激活函数

$$f(x)=max(0,x)$$

3.11 贝叶斯规则

$$P(x|y)=\frac{P(x)P(y|x)}{P(y)}$$

3.12 连续型变量的技术细节

测度论
零测度
几乎处处
Jacobin矩阵

3.13 信息论

量化信息

非常可能发生的事件信息量要比较少，并且极端情况下，确保能够发生的事件没有信息量
较不可能发生的事件具有更高的信息量
独立事件应具有增量的信息。例如，投掷的硬币两次正面朝上传递的信息量，应该是投掷一次硬币正面朝上信息量的两倍

定义一个事件X=x的自信息为
$$I(x)=-logP(x)$$
log为自然对数，底为e，I(x)单位是奈特，一奈特是以1/e概率观测到一个事件时获得的信息量
若以2为底数，单位是比特或者香农

香农熵，一个分布的香农熵时指遵循这个分布的事件所产生的期望信息总量
$$H(x)=\mathbb{E}_ {x\sim P}[I(x)]=-\mathbb{E} _ {x \sim P}[logP(x)]$$

当x连续，香农熵被称为微分熵

KL散度，用域衡量两个分布的差异
$$D_{KL}(P||Q)=\mathbb{E} _ {x \sim P}[log\frac{P(x)}{Q(x)}]=\mathbb{E} _ {x \sim P}[logP(x)-logQ(x)]$$

交叉熵
$$H(P,Q)=-\mathbb{E}_ {x \sim P} logQ(x)$$

3.14 结构化概率模型

结构化概率模型，又叫图模型

有向
无向

第四章数值计算

4.1 上溢和下溢

通过有限数量的位表示无限多的实数，总会引入舍入误差，包括了上溢和下溢
对上溢和下溢进行数值稳定的一个例子是softmax函数
$$softmax(x) _ i=\frac{exp(x_i)}{\sum_{j=1}^nexp(x_j)}$$

4.2 病态条件

条件数表征函数相对于输入的微小变化而变化的快慢程度
考虑函数$f(x)=A^{-1}x$，当A∈$\mathbb{R}^{n×n}$具有特征分解时，其条件数为
$$\max_{i,j}|\frac{\lambda_i}{\lambda_j}|$$

4.3 基于梯度的优化方法

（1）优化
大多数深度学习算法涉及某种形式的优化，包括改变x以最小化或最大化某个函数f(x)。通常以最小化指代大多数最优化问题，最大化可以经由-f(x)来实现

目标函数（准则）：要最小化或最大化的函数
代价函数（损失函数/误差函数）：对其进行最小化时也称之为代价函数

梯度下降：将x往导数反方向移动来减小f(x)

$\frac{df(x)}{x}=0$的点称为临界点，驻点
有些临界点既不是最大点也不是最小点，被称为鞍点

（2）偏导，梯度，方向导数
对于多维输入函数，提出了偏导数。偏导数为函数在每个位置处沿着自变量坐标轴方向上的导数（切线斜率）

梯度，写作$\nabla_xf(x)$，当前位置的梯度方向，为函数在该位置处方向导数最大的方向，也是函数值上升最快的方向，反方向为下降最快的方向。当前位置的梯度长度（模），为最大方向导数的值

方向导数，如果是方向不是沿着坐标轴方向，而是任意方向，则为方向导数

4.3.1 梯度之上：Jacobin和Hessian矩阵

1.Jacobin
在向量分析中, 雅可比矩阵是一阶偏导数以一定方式排列成的矩阵, 其行列式称为雅可比行列式. 还有, 在代数几何中, 代数曲线的雅可比量表示雅可比簇：伴随该曲线的一个代数群, 曲线可以嵌入其中.

雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近. 因此, 雅可比矩阵类似于多元函数的导数.
$$\begin{bmatrix}
\frac{\partial y_1}{\partial x_1} &\cdots& \frac{\partial y_1}{\partial x_n} \
\vdots & \ddots & \vdots \
\frac{\partial y_m}{\partial x_1} &\cdots& \frac{\partial y_m}{\partial x_n}
\end{bmatrix}$$

2.Hessian
在数学中, 海森矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵, 此函数如下：
$f(x_1,x_2,\cdots,x_n)$，如果f的所有二阶导数都存在，那么
$$\begin{bmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} &\cdots& \frac{\partial^2 f}{\partial x_1 \partial x_n} \
\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} &\cdots& \frac{\partial^2 f}{\partial x_2 \partial x_n} \
\vdots & \vdots & \ddots &\vdots\
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} &\cdots& \frac{\partial^2 f}{\partial x_n^2}
\end{bmatrix}$$

Hessian矩阵等价于梯度的Jacobian矩阵
海森矩阵在牛顿法中的应用，牛顿法时一个基于二阶泰勒展开来近似x附近的f(x)的方法

例如：在x0处展开
$$f(x)=f(x_0)+(x-x_0)^T\nabla_xf(x_0)+\frac{1}{2}(x-x_0)^TH(f)(x_0)(x-x_0)$$
临界点为
$$X’=X_0-H(f)(x_0)^{-1}\nabla_xf(x_0)$$

4.4 约束优化

在x的某些集合S中找f(x)的最大值或最小值，称为约束优化

Karush-Kuhn-Tucker（KKT）方法

广义Lagrangian（广义Lagrange函数）,通过m个函数g和n个函数h描述S，那么S可以表示为$\mathbb{S}={x|\forall i,g^{(i)}(x)=0 and \forall j ,h^{(j)}(x)≤0}$，其中涉及g的等式称为等式约束，涉及h的不等式称为不等式约束，定义如下：
$$L(x,\lambda , \alpha)=f(x)+\sum_i\lambda_ig^{(i)}(x)+\sum_j\alpha_jh^{(j)}(x)$$

4.5 实例：线性最小二乘

假设我们希望最小化下式中的x值：

$$f(x)=\frac{1}{2}\left|Ax-b\right| _ 2 ^ 2$$

首先，计算梯度
$$\nabla_xf(x)=A^T(Ax-b)=A^TAx-A^Tb$$

假设希望最小化同样的函数，但受$x^Tx≤1$的约束
$$L(x,\lambda)=f(x)+\lambda(x^Tx-1)$$

现在，我们解决以下问题
$$\min_x\max_{\lambda , \lambda ≥ 0}L(x,\lambda)$$

我们可以用Moore-Penrose伪逆。
关于x对Lagrangian微分，得到
$$A^TAx-A^Tb+2\lambda x=0$$

解为：
$$x=(A^TA+2\lambda I)^{-1}A^Tb$$

观察
$$\frac{\partial}{\partial \lambda}L(x,\lambda)=x^Tx-1$$

当x的范数超过1时，该导数是正的，所以为了跟随导数上坡并相对λ增加Lagrangian，我们需要增加λ。因为$x^Tx$的惩罚系数增加，秋节关于x的线性方程现在将得到具有较小范数的解

第五章机器学习基础

5.1 学习算法

能够从数据中学习的算法

5.1.1 任务T

通常机器学习任务定义为机器学习系统应该如何处理样本。
样本是我们从希望机器学习系统处理的对象或事件中收集到的已经量化的特征的集合

常见任务：分类，输入缺失分类，回归，转录，机器翻译，结构化输出，异常检测，合成和采样，缺失值填补，去噪，密度估计或概率质量函数估计

5.1.2 性能度量P

为了评估机器学习算法的能力，提出准确率，错误率

使用测试集数据来评估系统性能，将其与训练机器学习系统的训练集数据分开