目标检测 | SSD,经典单阶段Anchor-Based目标检测模型
1. 论文信息
论文标题: 《SSD: Single Shot MultiBox Detector》
论文发表:2016
论文链接:SSD: Single Shot MultiBox Detector | SpringerLink
1 | @inproceedings{liu2016ssd, |
2. 归纳总结
| 标签 | 目的 | 方法 | 总结 |
|---|---|---|---|
| #Anchor #单阶段 | 实现多尺度以及卷积预测,进一步提升精度和速度 | MultiBox,Anchor | 经典单阶段算法 |
3. 引言
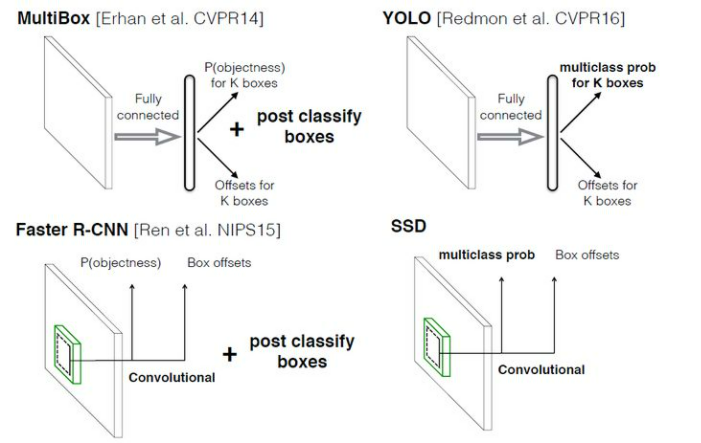
SSD算法,其英文全名是Single Shot MultiBox Detector, SSD的优势在于消除了bounding box proposal和pixel or feature resampling,并使用了multi-scale,因此达到了比faster rcnn和yolo更高的检测精度和更快的检测速度。
图片来自目标检测|SSD原理与实现 - 知乎 (zhihu.com)
4. SSD模型
SSD采用VGG16作为基础模型,然后在VGG16的基础上新增了卷积层来获得更多的特征图以用于检测,模型结构如下图:
SSD和Yolo一样都是采用一个CNN网络来进行检测,但是却采用了多尺度的特征图,网络的核心点:
- 使用小的卷积核预测类别和边界框偏移量
- 对多个(多尺度)特征图进行检测
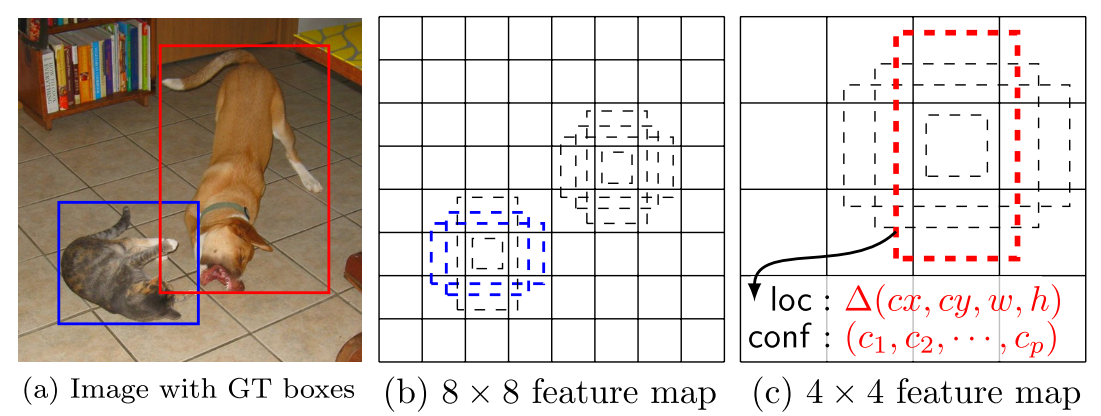
- 设置不同比例的先验框,如下图
SSD将背景也当做了一个特殊的类别,如果检测目标共有c个类别,SSD其实需要预测c+1个置信度值,其中第一个置信度指的是不含目标或者属于背景的评分。在预测过程中,置信度最高的那个类别就是边界框所属的类别,特别地,当第一个置信度值最高时,表示边界框中并不包含目标。第二部分就是边界框的location,包含4个值(cx,cy,w,h),分别表示边界框的中心坐标以及宽高。但是真实预测值其实只是边界框相对于先验框的转换值。先验框位置用$d=(d^{cx},d^{cy},d^{w},d^{h})$表示,其对应边界框用$b=(b^{cx},b^{cy},b^{w},b^{h})$表示,那么边界框的预测值$l$其实是b相对于d的转换值:
5. 模型训练
5.1 正负样本划分
首先,对于图片中每个ground truth,找到与其IOU最大的先验框,该先验框与其匹配,这样,可以保证每个ground truth一定与某个先验框匹配。通常称与ground truth匹配的先验框为正样本,其次,通过判断先验框和ground truth之间的IoU值是否大于阈值(如0.5),大于则为正样本
5.2 损失计算
损失包含两个部分:定位损失和分类损失
$$L(x,c,l,g)=\frac{1}{N}(L_{conf}(x,c)+\alpha L_{loc}(x,l,g))$$
其中N代表所匹配的正负样本数量,l代表预测框,g代表真实框,和faster rcnn相似,回归的偏移量的值是边界框的中心坐标(cx,cy)和框的宽度w和高度h。
$$\hat{g} _ {j}^{cx}=(g _ {j}^{cx}-d _ {i}^{cx})/d _ {i}^{w}$$
$$\hat{g} _ {j}^{cy}=(g_{j}^{cy}-d_{i}^{cy})/d_{i}^{h}$$
$$\hat{g} _ {j}^{w}=\log(\frac{g_{j}^{w}}{d_{i}^{w}})$$
$$\hat{g} _ {j}^{h}=\log(\frac{g_{j}^{h}}{d_{i}^{h}})$$
因此定位损失函数为:$L_{loc}(x,l,g)=\sum_{i \in Pos}^N \sum_{m\in {cx,cy,w,h}}x_{ij}^{k}smooth_{L1}(l_i^m-\hat{g} _ j^m)$
分类损失是一个softmax损失:$L_{conf}(x,c)=-\sum_{i\in Pos}^{N}x_{ij}^p\log(\hat{c} _ i^p)-\sum _ {i\in Neg}log(\hat{c} _ i^0)$
其中$\hat{c} _ i^p=\frac{exp(c_i^p)}{\sum_p(exp(c_i^p))}$